２つの正弦波の位相差を求める方法-02

位相が異なる正弦波の二次元プロット

2つの正弦波，を以下のように設定します

\(\Large x = x_0 \cdot sin \ ( \omega t) \)　

\(\Large y = y_0 \cdot sin \ ( \omega t + \phi ) \)　

ここで，それぞれの振幅は既知なので，振幅を規格化して，１とします．したがって，

\(\Large x = sin \ ( \omega t) \)　

\(\Large y = sin \ ( \omega t + \phi ) \)　

ここで，

\(\Large u = \omega t + \frac{\phi}{2} \)　

とすると，

\(\Large x = sin \ ( u - \frac{\phi}{2}) \)　

\(\Large y = sin \ ( u + \frac{\phi}{2} ) \)　

となります．

三角関数の公式，

\(\Large sin(x+y) = sin \ x \cdot cos \ y + cos \ x \cdot sin \ y\)　

\(\Large sin(x-y) = sin \ x \cdot cos \ y - cos \ x \cdot sin \ y\)　

から，

\(\Large x = sin ( u - \frac{ \phi}{2}) = sin \ u \cdot cos \frac{ \phi}{2} - cos \ u \cdot sin \frac{ \phi}{2} \)

\(\Large y = sin ( u + \frac{ \phi}{2})= sin \ u \cdot cos \frac{ \phi}{2} + cos \ u \cdot sin \frac{ \phi}{2} \)

となります．ここから変形していくのですが，ちょっとズルをして，結果をもとに計算していきます．それは，
　XYプロットは楕円体となる．
　45度傾いている
を既知の事実として考えていきます．

回転の公式は，

\(\Large X = x \cdot cos \ \theta - y \cdot sin \ \theta \)

\(\Large Y = x \cdot sin \ \theta + y \cdot cos \ \theta \)

ですが，ここで，θ=45度，と言う前提で進めると，

\(\Large X = \displaystyle \frac{x-y}{ \sqrt{2}} = \displaystyle -2 \ \frac{cos \ u \cdot sin \frac{ \phi}{2}}{ \sqrt{2}} = - \sqrt{2} \ sin \frac{ \phi}{2} \cdot cos \ u \)

\(\Large Y = \displaystyle \frac{x+y}{ \sqrt{2}} = \displaystyle 2 \ \frac{sin \ u \cdot cos \frac{ \phi}{2}}{ \sqrt{2}} = \sqrt{2} \ cos \frac{ \phi}{2} \cdot sin \ u \)

となります．ここで，

\(\Large a \equiv - \sqrt{2} \ sin \frac{ \phi}{2} \)

\(\Large b \equiv \sqrt{2} \ cos \frac{ \phi}{2}\)

とすると，

\(\Large X = a \cdot cos \ u　\)

\(\Large Y = b \cdot sin \ u \)

となり，

\(\Large \displaystyle \frac{X^2}{a^2} + \frac{Y^2}{b^2} = cos^2 u + sin^2u =1 \)

となり，楕円となることがわかります．つまり，最初のx,y,　は45度傾いた楕円となるのです．

a, b,が楕円の長軸，短軸の長さとなります．

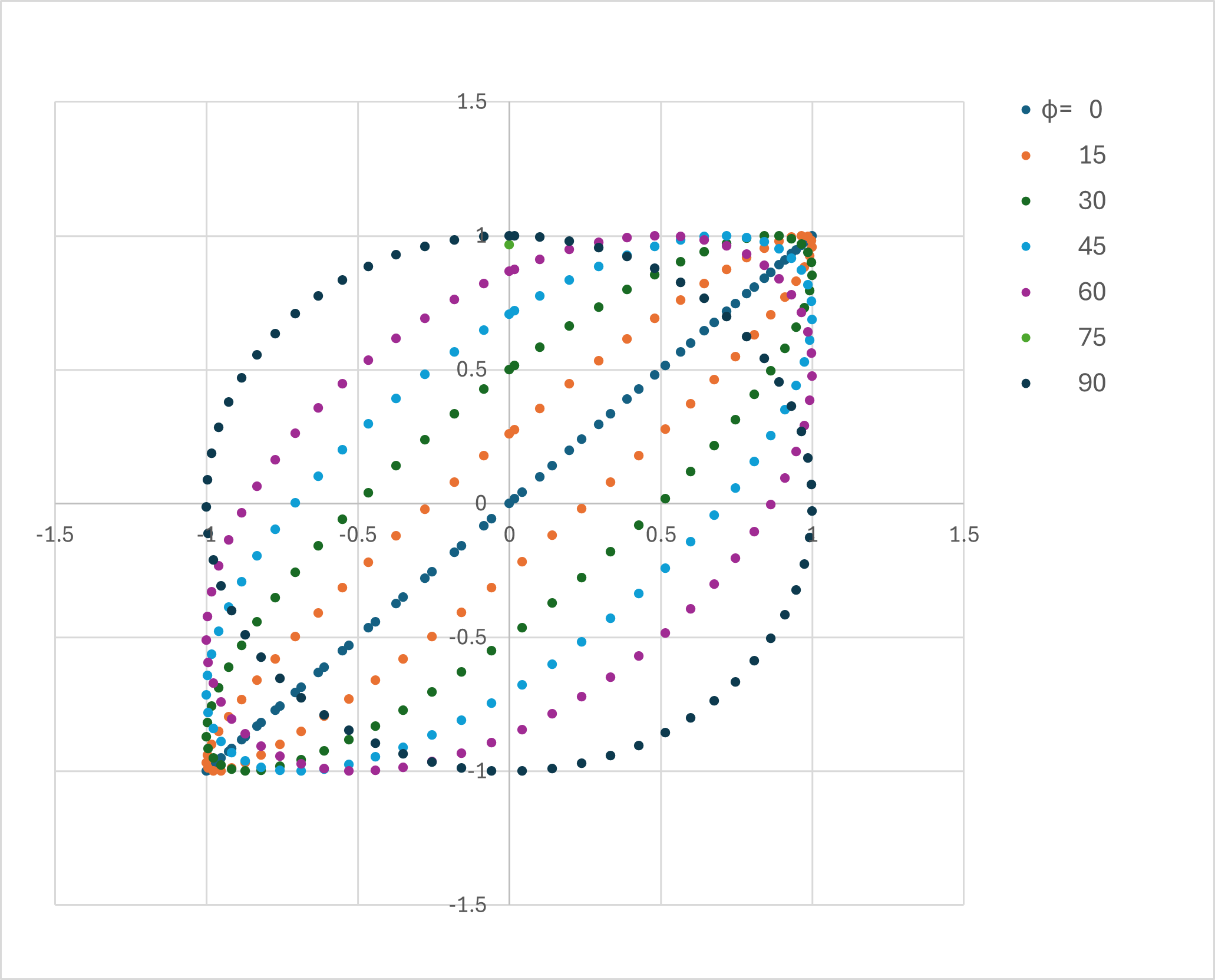
位相を変えてXYプロットを取っていくと，

となり，
　位相が0度：直線
　位相が90度：円
となります．

この長軸，短軸の式に位相が入っているので，ここから位相を推定できますが，これも結構面倒な導出となります．

次ページから，計算を簡単にするために，ベクトル積と面積との関係，を導入していきます．